El efecto Mpemba es un fenómeno por el que un líquido caliente puede congelarse más rápido que uno frío, bajo ciertas condiciones.
Este hecho, contraintuitivo, se conoce, al menos, desde la época de Aristóteles, hace unos 2.300 años. Fue redescubierto por Erasto Mpemba, estudiante de secundaria de Tanzania, quien, junto con el físico Denis Osborne, lo investigó, por primera vez, en la década de 1960. Su artículo, publicado en 1969 en Physics Education, se tituló apropiadamente “Cool?” (¿frío?, en inglés). Hace pocos meses se convirtió en una tendencia viral en redes sociales, que consistía en lanzar al aire agua hirviendo para ver cómo se congela rápidamente y se transforma en nieve.
Ha habido cierta controversia con respecto a este fenómeno, ya que ha resultado difícil replicar consistentemente el resultado en laboratorio. Los detalles más pequeños tienen gran importancia, como el tamaño, la forma y el material del recipiente, o incluso dónde se coloca el termómetro. Se han propuesto varias explicaciones para el efecto Mpemba: convección, evaporación, sobre enfriamiento, impurezas en la muestra de agua, gases disueltos, etc. No existe un argumento comúnmente aceptado, todos los fenómenos anteriores parecen intervenir.
Además, aunque estas explicaciones pueden ser parcialmente ciertas para el agua, no consiguen explicar el fenómeno para otras sustancias, como aleaciones de magnetorresistencia, aleaciones de polímeros y sistemas granulares, donde también se observa. En un estudio de 2017 se ofrece una explicación teórica general de este fenómeno, utilizando la teoría de la termodinámica del no equilibrio.
De acuerdo a esta teoría, cualquier punto en el espacio de fases de un fluido en equilibrio puede describirse con tres números: su temperatura, volumen y número de partículas. Sin embargo, cuando el fluido está en proceso de enfriamiento, no está en equilibrio y la cantidad de estados requeridos para describir el sistema aumenta a infinitas dimensiones, por lo que se necesitan infinitos números para cuantificar con precisión cuál es el estado del fluido.
Cuando un líquido caliente se coloca en un ambiente frío, trata de alcanzar su estado de energía más bajo. Sin embargo, el panorama energético definido en sus estados tiene múltiples mínimos locales —es decir, puntos que toman valores menores que los de su alrededor—, llamados pozos de energía metaestable. Si un líquido caliente entra en estos pozos de energía metaestable, tiene más energía para escapar más fácilmente de él y encontrar el mínimo global —la temperatura de enfriamiento—, mientras que, si un líquido más frío entra en uno de los pozos de energía metaestable, pasará más tiempo en él.
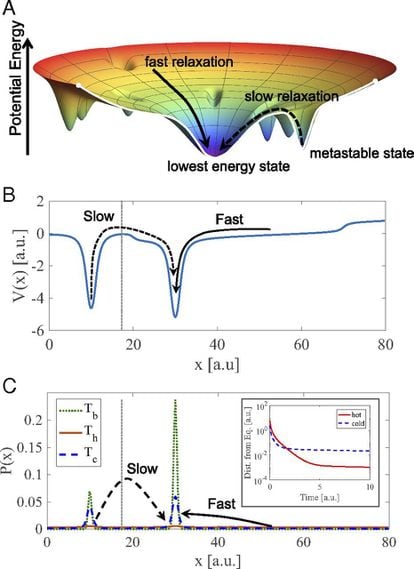
Con más precisión, se puede modelar el estado del sistema mediante una función de distribución de probabilidad, que describe las probabilidades de todos los posibles estados que podría tener, cuya evolución se rige por una ecuación diferencial lineal. Para un sistema con estados finitos, esta evolución está determinada por las propiedades de la llamada matriz de transición. Ahora, para este tipo de sistema, cualquiera que sea la distribución de probabilidad inicial, convergerá, en algún momento, al estado de equilibrio. Sin embargo, debido a la forma de la matriz de transición, existe una función de distribución de probabilidad especial que convergerá al estado de equilibrio a la velocidad más lenta posible, en comparación con todas las demás distribuciones de probabilidad iniciales.
Así, para observar el efecto Mpemba, necesitamos que la distancia de la función de distribución de probabilidad al estado de equilibrio sea más pequeña para el líquido más caliente, en comparación con el líquido más frío, después de algún tiempo. Esto puede suceder si, inicialmente, la función de distribución de probabilidad para el líquido más frío está más cerca de esta función de distribución de probabilidad especial, que la del líquido más caliente. Esto dará como resultado que el líquido más frío converja al estado de equilibrio más lentamente que el líquido más caliente, después de algún tiempo.
Unos científicos predijeron un efecto Mpemba inverso: que cuando dos líquidos se calientan, el más frío puede calentarse más rápido. Fenómeno observado ahora en experimentos
Usando este análisis, los autores del artículo predijeron un efecto Mpemba inverso, en el que cuando dos líquidos se calientan, el más frío puede calentarse más rápido. Este fenómeno se ha observado ahora en experimentos. En un estudio teórico de 2019 que utilizó un enfoque similar, los físicos también predijeron el efecto Mpemba fuerte en el que, bajo parámetros cuidadosamente elegidos, el líquido más caliente puede enfriarse exponencialmente más rápido en comparación con el líquido frío inicial. Esto también se ha observado experimentalmente.
Sin embargo, el efecto Mpemba para el agua sigue sin resolverse, y tendremos que esperar unos años más para obtener una respuesta definitiva a esta pregunta.
Siddhant Govardhan Agrawal es investigador postdoctoral en el ICMAT.
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
