El problema de Hadwiger-Nelson es posiblemente uno de los más conocidos del área de la geometría discreta. Se trata de la siguiente cuestión: ¿cuál es el número mínimo de colores que se necesitan para pintar el plano, de tal modo que siempre, al tomar dos puntos cualesquiera, con una distancia de una unidad entre ellos, estos hayan sido pintados con colores distintos? Aun siendo una pregunta aparentemente inocente, lleva sin respuesta más de 70 años. Sin embargo, gracias a herramientas de aprendizaje automático, recientemente se ha conseguido avanzar en su comprensión.
Hasta el momento, se sabe que el número de colores necesarios puede ser cinco, seis o siete. Para estudiar el número mínimo de colores necesarios, basta con encontrar configuraciones concretas de puntos en el plano que no puedan pintarse con un número –llamémosle n– de colores y cumplir la propiedad indicada. Así, sabemos que necesitamos más, al menos, n+1 colores para pintar el plano completo –que incluye ese dibujo específico–, si queremos que se verifique la propiedad.
En primer lugar, es fácil ver que, como mínimo, hacen falta tres colores. Efectivamente, tomando una disposición tan sencilla como los tres vértices de un triángulo equilátero cuyo lado mide uno, ya necesitamos tres colores para colorearlos, de forma que no haya dos vértices adyacentes con el mismo color –si no, estos puntos no cumplirían la propiedad buscada: estarían a distancia 1 y tendrían el mismo color–.
Refinando este tipo de argumento, a principios de los años 60 del siglo pasado, los hermanos Leo y William Moser encontraron una configuración concreta de solo siete puntos del plano que necesita al menos cuatro colores para cumplir la propiedad que queremos, lo que demuestra que el número mínimo es cuatro. Más recientemente, en el año 2018, el matemático aficionado Aubrey de Grey encontró una configuración con más de 1000 puntos del plano en la que era necesario, como mínimo, usar cinco colores para que se cumpliera la condición deseada.
Además, se sabe que el número de colores no puede ser más que siete, porque conocemos estrategias para colorear con estos colores el plano que consiguen nuestro objetivo. Por ejemplo, basta tomar una teselación en forma de panal de abejas y pintar un hexágono de un color y los seis adyacentes de colores diferentes. Como el diámetro de cada hexágono es inferior a ½, dos puntos cualesquiera a distancia, uno caen siempre en hexágonos diferentes, adyacentes, por tanto, pintados de diferente color.
Pero esto no resuelve el misterio, podría haber otra coloración, que todavía no conozcamos, que requiera menos colores y siga cumpliendo la propiedad. Así pues, la respuesta puede ser cinco, seis o siete y, de momento, nadie sabe cómo resolver este enigma.
Para seguir avanzando en la investigación, una estrategia habitual en matemáticas es imponer restricciones más débiles y resolver el problema resultante. Esto, muchas veces, permite encontrar enfoques para solucionar la pregunta original. En nuestro caso, para estudiar el problema de Hadwiger Nelson débil, analizamos qué pasa si permitimos que algunos de los puntos pintados de un mismo color estén a una distancia diferente a uno. Para ello, introducimos la noción de configuración válida de una coloración del plano de n colores, con distancias (d1, d2, … dn) asociadas a cada color.
Por ejemplo, si n=4, los colores son azul, verde, amarillo y naranja, y las distancias 1,5 –asociada al color azul–, 0,2 –al verde–, 1 –al amarillo–, 3,7 –al naranja–, una configuración válida con estos valores es un conjunto de puntos en los que toda pareja de puntos coloreada con el mismo color está a una distancia mayor que la distancia asociada a ese color. En el ejemplo, no puede haber dos puntos azules a menos de 1,5 de distancia o dos verdes a menos de 0,2.
Así, encontrar una configuración válida de seis colores con distancias asociadas (1,1,1,1,1,1) supondría demostrar que la respuesta al problema de Hadwiger-Nelson es, como mucho, seis. Encontrar una configuración de cinco colores y con distancias (1,1,1,1,1) sería incluso mejor, ya que resolvería completamente el problema. Y, aun siendo menos ambiciosos, hallar configuraciones de este tipo permite aumentar nuestro conocimiento sobre el problema general.

Recientemente, un equipo de investigadores del Zuse Institute Berlin (ZIB) y de la Technische Universität Berlin (TU Berlin) han obtenido un avance en esta dirección. Konrad Mundinger, Sebastian Pokutta, Christoph Spiegel y Max Zimmer han dado con una configuración válida de seis colores (1,1,1,1,1,d), donde el valor de d está entre 0,354 y 0,657. Dicho de otro modo, los puntos coloreados con los cinco primeros colores mantienen la condición con una distancia unidad, mientras que para el sexto color se relaja la condición: puede haber un par de puntos pintados de este color a una distancia menor, entre 0,354 y 0,657. Este resultado mejora resultados previos del año 1996, ampliando el margen de posible elección para d.
Pero, además, lo que es realmente interesante es el papel que ha jugado el aprendizaje automático en la obtención de este resultado. Su idea, a grandes rasgos, ha sido entrenar una red neuronal para encontrar representaciones que cumpliesen las condiciones deseadas, intentando que el valor de d fuera lo mayor posible. Este tipo de redes neuronales no son capaces de resolver el problema de manera exacta, sino que obtienen propuestas de soluciones aproximadas, testeando un enorme número de combinaciones posibles, lo que resulta una tarea inalcanzable para el ser humano.
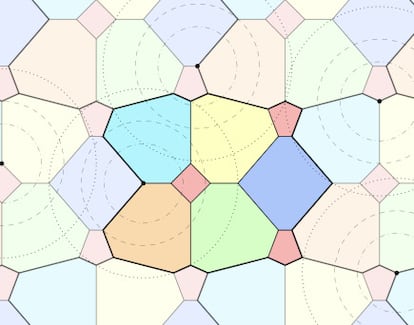
Entonces, la red neuronal funciona a modo de “oráculo aproximado”, y es trabajo de los investigadores interpretar la información generada y dar forma a esta vía de exploración en una posible solución. Con estas técnicas los autores han sido capaces de obtener diversas construcciones que mejoran todas las conocidas hasta el momento. Por ejemplo, han construido una teselación de tipo periódica (en la imagen) que usa seis colores, en la que el sexto color, el rojo, es el que cumple con las condiciones más laxas.
Este tipo de técnicas computacionales son muy prometedoras y es posible que en el futuro permitan tratar otros problemas que hoy en día son inabordables, como, por ejemplo, el estudio del mismo problema en el espacio –en lugar del plano–, o el problema de Hadwiger-Nelson en su totalidad.
Juanjo Rué es profesor agregat del Departamento de Matemáticas de la Universitat Politècnica de Catalunya (UPC), miembro del Instituto de Matemáticas de la UPC (IMTech) e investigador adscrito al Centre de Recerca Matemàtica (CRM).
Ágata A. Timón G Longoria, coordinadora de la Unidad de Cultura Matemática del ICMAT.
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Edición, traducción y coordinación: Ágata Timón García-Longoria. Es coordinadora de la Unidad de Cultura Matemática del Instituto de Ciencias Matemáticas (ICMAT)
